在许多金相试样中都能观察到具有一定取向的微观组织，如果该组织是由机加工或经特殊温度热处理工艺等宏观机制引发的，那么其分布状态将具有整体性。比如，轧制双相不锈钢中的铁素体-奥氏体组织和轧制钢中的珠光体。在上述情况下，带状组织使材料产生各向异性。此外，一些性能也会被削弱，比如加工性能、氢致裂纹萌生与发展、在带状珠光体区焊接时热影响区(heat-affected zone，HAZ)的裂纹倾向性等。Anders From和Rolf Sandstrom将基于频谱分析技术的现代图像处理方法用于带状组织的无损评价。方法1是用局部傅里叶变换来提取局部优势取向，局部取向分布方程可以表示所有方位角的分布。方法2和方法3是基于全局傅里叶变换的处理方法。其中方法2是利用在两相互垂直方向傅里叶频谱灰度分布的不同对带状组织进行定量。在方法3中研究了定向图像能量与取向之间的函数关系，用灰度变化定义的图像能量等于傅里叶频谱的平方，引入了能量分布的概念。本文推荐的各种方法都是Komenda和Sandstrom所创建方法的延续，Komenda 和Sandstrom都是以Feret斜率或弦斜率来对带状组织进行评价的。这些方法已在带状珠光体钢和铁素体-奥氏体双相不锈钢两类材料中得到了成功应用。

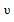在通常的灰度圖中，可以將對比度作爲幾何位置的函數，即將相應頻譜所對應的兩個實部的數值分列于相互垂直的坐標軸上，由二維傅裏葉變換處理得到的圖像具有極高的完整性和精確性。在頻率空間內二維傅裏葉變換可以用極坐標F( ,ψ)表示。一般來說，頻率爲 ，方向角爲ψ。如果用灰度代表函數F( 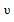 ,ψ)，那麽F( 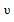,ψ)的值由頻率 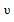和方向角ψ共同決定，且頻率分布由方向角ψ確定。ψ值則可以處于原圖像上所有可能的位置，經轉換處理後圖像上的每一點都包含了原圖中所有點的信息。應該引起注意的是：在轉換的過程中不會丟失信息，所以逆傅裏葉變換可以精確得到原始圖。

傅裏葉變換的優勢是重排機制。在頻譜F(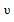 ,ψ)中，幅度的高低取決于指定頻率和方位上信息的強弱。灰度高，幅度就高，圖像上顯示爲亮度，所以圖中亮度高的區域代表頻率和方位的優勢區域。特別是當材料的微觀組織受晶粒取向、帶狀組織以及某種微觀各向異性的共同作用産生方向性時，頻譜圖上則出現亮區。事實上，頻譜中的各向異性與原始灰度圖中的各向異性相互印證。頻率圖中有關各向異性的定量分析尚未完成。以下給出了有關單值參量的三種處理方法。

可以创建一个数字图像过滤器用于提取材料的强度和取向，这种过滤模式的图像分析系统之一是GOP系统，将分布函数作为每个指定的图像点周围指定取向上图像点的数目。文中对这类分布函数叫作局部取向分布函数( Local Orien-tation Distribution Function, LODF)。

正交频率分布( orthogonal frequency distribution，OFD)定义为两个垂直方向上傅里叶变换的差值，是一种定量评价钢中带状组织和择优取向组织的新方法。如果这个差值在一个方向上是周期性的，在傅里叶频谱的相应频率上就会出现一个OFD峰值；如果在第一方向有规律性的变化，OFD的实部则在对应的频率位置出现一个峰值；如果在第二方向有规律性的变化，OFD图中会有一个凹陷。正是OFD的这一特性使之适用于分析带状组织的数量和取向。

傅裏葉譜的局部能量用幅度的平方表示，如果局部能量是在指定方向角ψ上所有點位的總和，這時局部能量則以E(ψ)表示，叫做能量分布函數(EDF)E(ψ)。在E(ψ)圖中，原圖中的優勢取向顯示爲一個凸峰，該峰值可用于原圖中取向度的評價。

有關圖8-14中材料微觀組織的頻譜F(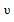 ,ψ)，如圖8-15所示，頻譜圖中將取向度給予了非常直觀的顯示，GOP—300系統可用于頻譜處理和隨後的一系列分析工作。圖像的像素是512x512，圖像的幅值分辨率爲16bit(例如灰度分爲2¹⁶=65536個級別)。圖8-16爲對圖8-12進行計算處理得到的正交頻率分布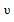P()圖，P(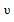 )值在±20MHz範圍以外接近零值，大部分值分布在±10MHz範圍內，此即所謂的S(10)值。研究表明：鋼的變形度越大，則其對應的S(10)值越大。

靈科超聲波堅持自主研發，最大力度投入研發設計，擁有一支近30年的研發制造團隊，發明創造170余項專利新技術。主要品牌有LINGGAO靈高、LINGKE靈科、SHENGFENG聲峰等。廣泛運用在醫療器械、電子器材、打印耗材、塑料、無紡布、包裝、汽配等多個領域，爲海內外各行業、企業提供了大量穩定性強的優質超聲波塑焊設備及應用方案。